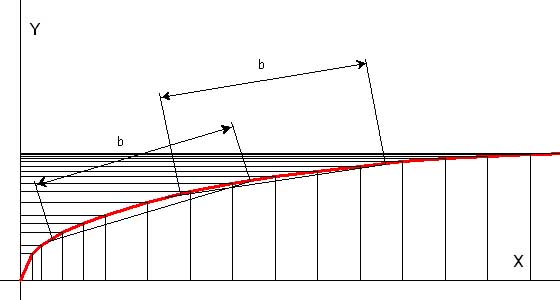
В целом течение можно представить так, будто винт каждой лопастью отрезает кусочки воды от общей массы, придавая им ускорение, а в образующиеся полости устремляется атмосферный воздух, который после такого перемешивания выходит из воды пузырями далеко за винтом.
Неискажённость потока учитывается в пункте 1 , где скорость лодки V постоянна для всех расчётных радиусов (постоянство поля скоростей).
В вверх.
1. Поступь винта.
Поступью винта Hп называется расстояние, проходимое винтом в воде, на расчётной скорости, за один оборот. Поступь винта зависит от оборотов двигателя nдв, редукции i, и скорости лодки V (скорость набегающего потока).

Для рассчёта поступи винта сначала задаются обороты двигателя. Затем, зная редукцию, можно определить число оборотов винта nв.
nв = nдв * i; (1.1)
nв = [об./мин.] * ( / ) = [об./мин.] (1.2)
поделив на 60, получим число оборотов в секунду
nв =[об./мин.] / 60 =[об./сек.]; (1.3)
Дальше определяется скорость лодки в метрах в секунду. Если исходить из показаний манометра, то скорость в [км./час.] определяется по формуле:
V[км./час.] = 50,2 * ( P[кг./см2] )1/2; (1.4)
Где P - показания манометра в [кг./см2];
Пример: P = 4 [ кг./см2];
V = 50,2 * ()1/2 =[ км./час. ]; (1.5)
Для того, чтобы скорость в [км./час.] перевести в метры в секунду, нужно её значение поделить на 3,6.
V [м./сек.] = V [км./час.] / 3,6; (1.6)
V =[км./час.] / 3,6 =[м./сек.]; (1.7)
Таким образом, получим, что за одну секунду лодка проходит м, а винт делает оборота. Значит за один оборот винт проходит расстояние
Hп = V / nв; (1.8)
Hп =[м./сек.] / [об./сек.] = [м.], (1.9)
То есть Hп = мм (поступь винта) или, примерно, Hп = мм.
В вверх.
2. Определение угла поступи.
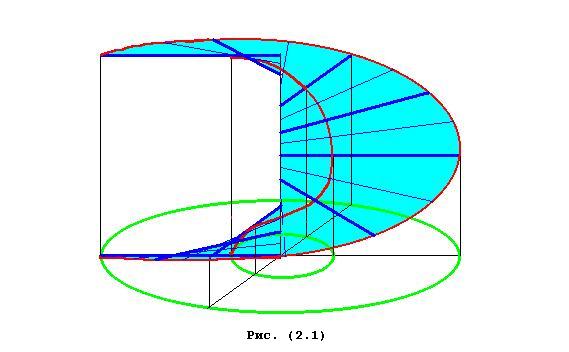
При пересечении винтовой поверхности с круговыми цилиндрами, оси которых совпадают с осью винтовой линии и имеют наперёдзаданные радиусы, получим семейство винтовых линий (Рис(2.1)).
Винтовая линия при развёртке каждого такого цилиндра будет гипотенузой прямоугольного треугольника с катетами Hп и 2*π*r (Рис.(2.2)).
где Hп - величина поступи [мм.]
r - радиус одного из цилиндров [мм.]
Угол α° называется углом поступи винта.Для каждого радиуса он будет свой.
По определению тангенса угла α°
tgα° = Hп/(2*Pi*r), (2.1)
α° = arctg(Hп/(2*Pi*r)) (2.2)
r = мм.; Hп = мм.;
α° = arctg(()/(2*Pi* )) = ° ; (2.3)
Для заданного радиуса (r = мм.)
Угол α° определяется для всех значений r, по которым строится шаговая горка.
Переход к таблице расчёта
В вверх.
3. Суперкавитирующий профиль.
Суперкавитирующий профиль и картина его обтекания изображены на рисунке (3.1).
Vоо - линия натекания потока воды.
Угол между хордой нагнетающй поверхности и вектором Vоо есть угол атаки профиля Δα°
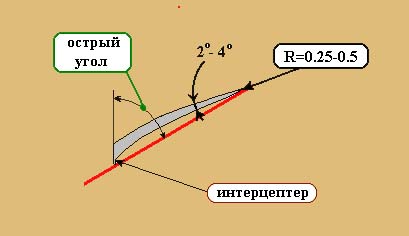
Входящая кромка имеет радиус закругления r = 0.25 - 0.5 мм.
У носика профиля угол атаки нагнетающей поверхности составляет 2° - 4°???.
Кривизна нагнетающей поверхности плавно нарастает от носика к выходящей кромке, для того чтобы эпюра давления нарастала по длине профиля и не было возможности возникновения кавитации на нагнетающей стороне.
Выходящая кромка составляет острый угол с хордой нагнетающей стороны, для того чтобы было легче наколотить интерцептор (для "затяжеления" винта в процессе его доводки.
Нагнетающую поверхность профиля можно строить по лекалу, изображённому на чертеже, отсекая хордой необходимый по длине отрезок, варьируя кривизну за счёт смещения отрезка по дуге вправо или влево.
Координаты лекальной линии приведены в таблице (3.1).
| Xmm. | 0 | 3 | 5 | 10 | 15 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ymm. | 0 | 6.5 | 8.3 | 11.3 | 13.5 | 15.5 | 18.5 | 21 | 23 | 24.5 | 25.7 | 27 | 28 | 28.8 | 29.3 | 29.8 | 30 |
Расчёт величины хорды приведен в пункте 5.
Лекало для построения шаговых угольников необходимо вырезать из металла. Построение шаговых угольников описывается в пункте 6.
Засасывающая сторона большого влияния не имеет. Она должна удволетворять лишь требованиям прочности и не создавать лишнего сопротивления, то есть иметь довольно острый угол с нагнетающей стороной ( 2° - 4° у носика профиля ).
В вверх.
4. Оптимальный угол атаки профиля и вычисление шага винта.
Хорда нагнетающей стороны профиля лопасти (при некотором r) образует с винтовой поверхностью поступи, параллельно которой происходит натекание потока на лопасть, некоторый угол Δα°.
Оптимальный угол атаки, с точки зрения гидродинамического качества профиля, зависит от шага решётки профилей и их формы, то есть от поступи Hп, числа лопастей z, радиуса r, длины профиля по хорде b, а также от формы профиля.
Для суперкавитирующего профиля оптимальным (в первом приближении) можно считать угол в 7° - 8°, для значений радиуса, заключённых между двумя величинами: радиусом ступицы rст и радиусом винта R.
Из чертежа видно, что
Hв / ( 2 π r ) = tg ( α° + Δα° ) (4.1)
Тогда шаг винта
Hв = ( 2 π r ) * tg ( α° + Δα° ) (4.2)
r = мм.; Δα° = ° ; α° = ° ;
Hв = ( 2 π ) * tg ( ° + ° ) = мм.
Для заданного радиуса (r = мм. (ошибочное значение шага винта.))
При расчёте шаговой горки шаг винта вычисляется для всех радиусов,на которые изготовляются шаговые угольники.
Переход к таблице расчёта
В вверх.
5. Понятие дискового отношения,
распределение хорды по радиусу.
Дисковое отношение Θ, это отношение суммы площадей спрямлённых поверхностей всех лопастей к площади диска винта.
z - число лопастей
D - диаметр винта
Sл - площадь спрямлённой поверхности лопасти
SD = ( π / 4 ) * D 2 (5.1)
SлΣ = z * Sл (5.2)
Θ = ( z * Sл ) / (( π/4) * D 2 ) (5.3)
При одном и том же дисковом отношении очертание лопасти может быть различным, в зависимости от распределения хорды лопасти по радиусу (Рис. (5.2)).
От очертания лопасти зависят некоторые динамические параметры винта.
r - ось радиусов лопастей
b - ось хорд лопастей
1, 2 и 3 - кривые, определяющие очертание лопасти и соответствующие им точки центров приложения сил.
На кривой 1 центр приложения силы смещён на больший радиус, то есть находится дальше от ступицы, чем на 2 и 3.
На кривой 3 центр приложения силы расположен ближе к ступице.
При равномерном распределении давления по поверхности лопасти центр приложения силы находится там же, где центр тяжести плоской пластинки такого же очертания. Такая аналогия уместна для обьяснения, но распределение давления не всегда рвномерно.
Таким образом, очертание лопасти влияет на динамическую центровку лодки на ходу. Например, винт, изготовленный с очертанием лопасти по кривой 1, будет при одной и той же установке мотора задавать больший кабрирующий момент (на взлёт), чем винт, изготовленный по кривой 3, потому что центр приложения силы упора винта будет глубже от поверхности воды.
Винт, имеющий очертание лопасти по кривой 1, будет иметь и больший упор, нежели винт 3, потому что работа, совершаемая силой упора, будет больше, так как центр приложения сил каждой лопасти по форме 1 при частичном погружении большее время находится в воде.
дуга 3 - траектория движенния центра приложения сил лопасти с очертанием по кривой 3.
дуга 1 - траектория движенния центра приложения сил лопасти с очертанием по кривой 1.
Для расчёта контура спрямлённой поверхности лонасти необходимо заполнить столбцы r и br таблицы (5.1).
| rb = r / R | Bb = br*z/D*Θ | ___r___ | ___br___ |
|---|---|---|---|
| 0,2 | 1,32 | ___ | ___ |
| 0,3 | 1,65 | ___ | ___ |
| 0,4 | 1,92 | ___ | ___ |
| 0,5 | 2,12 | ___ | ___ |
| 0,6 | 2,28 | ___ | ___ |
| 0,7 | 2,32 | ___ | ___ |
| 0,8 | 2,25 | ___ | ___ |
| 0,9 | 1,96 | ___ | ___ |
| 0,95 | 1,62 | ___ | ___ |
| 1,00 | 0,00 | ___ | ___ |
( Таблица из книги "Гребные винты для катеров", Хейфец Л.Л. )
где rb - безразмерный радиус
Bb - безразмерная хорда
Таблица заполняется по следующим формулам:
r = rb * R; (5.4) br = bb * ((D * Θ)/z); (5.5)
где D - диаметр винта [mm.]
R - радиус винта [mm.]
Θ - дисковое отношение (задаётся)
В нашем примере Θ = 0,5
z - число лопастей
На графике нанесены две сетки радиусов. По сетке радиусов из таблицы (5.1) строится график зависимости br ( r ) , а по сетке радиусов для таблицы (5.2), с графика снимаются значения br ( r ) для занесения их в таблицу (5.2).
Сетка радиусов таблицы (5.1) находится в процессе вычисления по предидущим формулам (5.4) и (5.5) при заполнении таблицы (5.1).
Сетка радиусов таблицы (5.2) определяется стандартными радиусами шаговой плиты, на которые изготовляются шаговые угольники. Шаговые угольники изготовляются для стандартных радиусов, значения которых лежат между значениями радиуса ступицы rст и радиуса винта R
Пример:
| ____r___ | 35 | 45 | 55 | 65 | 75 | 85 | 95 | 105 | 115 |
|---|---|---|---|---|---|---|---|---|---|
| ___br___ | ______ | ______ | ______ | ______ | ______ | ______ | ______ | ______ | ______ |
Для расчёта винтов с другой формой лопастей, отличной от описанной в книге "Гребные винты для катеров", можно пользоватся таблицами, подобными таблице (5.1), но с другими числовыми значениями Bb, или заполнять сразу таблицу (5.2), имея данные с винта прототипа, или же заполнять таблицу (5.2), используя при этом теоретические зависимости.
В вверх.
6. Расчёт шаговых угольников.
Имея вышеописанные данные, можно приступить к расчёту шаговых угольников.
Заданными были:
D - диаметр винта [mm.]
dст - диаметр ступицы [mm.]
z - число лопастей
Θ - дисковое отношение
Hп - поступь вычисленная в пункте 1 (формула (1.9)).
Δα° - угол атаки профиля 7° - 8°
br - ширина лопасти по хорде (табл.(5.2))
r - сетка радиусов шаговой плиты (таблица (5.2)).
Пример рассчёта шаговых угольников винта "Вихрь-30", "SC" - катамаран.
Таблица (6.1).
* Красным
цветом выделены величины, используемые для построения чертежа шагового угольника.
Строки таблицы (6.1) с (5) по (13) заполняются в порядке расчёта по нижеследующим формулам. Расчёт ведётся по столбцам.
(5) = arctg((2)/(2π*(1));
(переход к тексту)
(6) = (5) + (4);
(переход к тексту)
(7) = 2π * (1) * tg(6);
(переход к тексту)
(8) = (3) * sin(6);
(9) = (3) * cos(6);
(10) = (8) + 20[mm];
(9) + 5[mm];
(12) = (9) * ( (2) / ( 2π * (1));
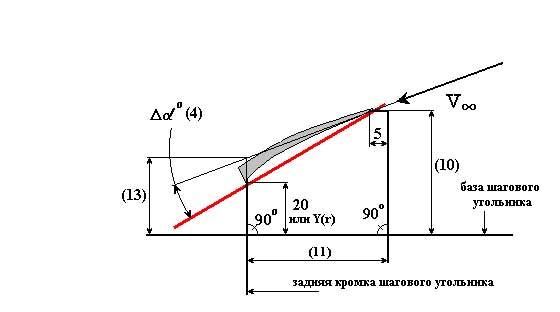
Шаговые угольники строятся по расчётным данным таблицы (6.1) из строчек (10), (11) и (13), а также размерам 20mm. и 5mm.
Размеры 20mm. и 5mm. - технологические. В данном примере размер 20mm. постоянен для всех радиусов шаговой горки. Если лопасти необходимо задать наклон в корму, то вместо размера 20mm необходимо ввести переменную величину задаваемую таблично.
Например:
| ___r___ | __35_ | __45_ | __55_ | __65_ | __75_ | __85_ | __95_ | _105_ | _115_ | (1) |
|---|---|---|---|---|---|---|---|---|---|---|
| __Y(r)__ | 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 | (14) |
Это введёт соответствующие изменения в результаты расчёта, т.к. строка (10) таблицы будет вычислятся по иной формуле
(10) = (8) + Y(r);
Далее расчёт вести по тем же формулам.
Параметр Δh строка (13) таблицы (6.1) позволяет отложить оптимальный угол атаки Δα° на чертеже шагового угольника, то есть провести линию натекания потока воды на данном радиусе.
(*)Кривая профиля отчерчивается по лекалу, таким образом, чтобы линия профиля не выходила за рамки угла Δα°, имела плавное сопряжение с линией натекания потока воды (1° - 3°) и достаточную кривизну. Кривизна профиля должна плавно наростать от точки входа к задней кромке лопасти.
Вырезанные из металла угольники, (обычно сталь толщиной 0,5 - 0,8 мм.) сверлят в нижней частии, как показано на (рис. 6.2)
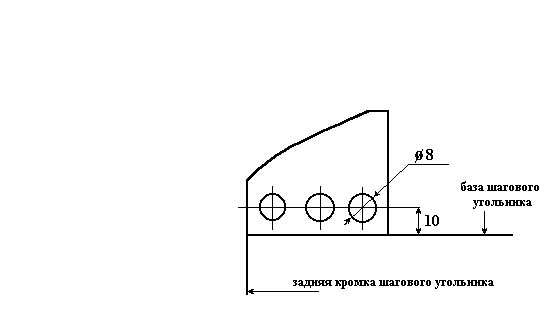
Затем их изгибают по соответствующим им радиусам, с учётом необходимого им направлени вращения, для установки на шаговой плите.
В вверх.
7. Изготовление шаговой горки.
Шаговые угольники выставляются на шаговой плите таким образом, что их задняя кромка проходит вдоль некоторой линии. Такой линией может быть линия радиуса, прямая линия расположенная под определённым углом к линии радиуса, или кривая линия, заданная по какому-то закону.
Если задние кромки угольников выставлены вдоль линии отличной от линии радиуса, то говорят, что лопасть имеет откидку. Для увеличения прочности лопастей им придают откидку до 20° против направления вращения винта. Теоретическое обоснование этого метода увеличения прочности лопастей приведено в [3] на страницах с 45 по 47.
Выставленные угольники заливают на высоту 20-25мм от основанияэпоксидной смолой, предварительно заизолировав шаговую плиту пластилином, и поставив вокруг шаговой горки пластилиновое ограждение.
Далее сверху эпоксидной смолы, после её затвердевания, горку залепляют пластилином и выравнивают полученный отпечаток поверхности лопасти по "рёбрам" шаговых угольников.
Таким образом, горка готова. По ней можно выклеивать модель лопасти винта, а также доводить поверхность лопастей отлитых винтов на прилегание.
В примере, приведённом в таблице (6.1), лопасть винта не имеет откидки и наклона в корму. Выходная кромка лопасти перпендикулярна линии оси винтовой пверхности.
В вверх.
8. Некоторые рекомендации и пояснения к доводке винтов,
изготовленных по такому методу.
По аналогу с винтом из примера, описанного в таблице (6.1), можно рассчитывать другие винты, внося изменения в исходные данные, то есть в строки (1), (2), (3) или (4), а также придавать лопасти наклон в корму и (или) откидку против направления вращения.
Если винт окажется лёгкий, то можно Δα° в строке (4) таблицы (6.1) принять 8° или увеличить поступь Hп в строке (2), или на готовый винт наколотить интерцептор. Затяжелить винт можно также увеличив дисковое отношение Θ и т. д.
Подобные винты, назовём их винтами с постоянным углом атаки профиля, (???) гораздо менее склонны к кавитации на нагнетающей поверхности лопасти, чем винты постоянного шага, потому что при вышеизложенном методе расчёта учитывается угол набегающего на винт потока и, практически входная кромка не затеняет даже частично поверхности лопасти, что часто ведёт к возникновению кавитации.
Если на корпусе катамарана перед редуктором установлен обтекатель, то он внесёт изменения в поле скоростей потока, набегающего на винт. Для этого нужно знать метод решения задачи об определении поля скоростей потока после обтекателя.
Это задача обтекания с отрывом струй тела вращения заданной формы в бесконечном потоке идеальной несжимаемой жидкости.
Обтекатель даст некоторое увеличение скорости воды, набегающей на близкие к ступице радиусы винта. Это приводит к неравномерному увеличению Hп на нескольких малых радиусах, в связи с ростом V (скорость набегающего потока) для малых радиусов (формула(1.8))
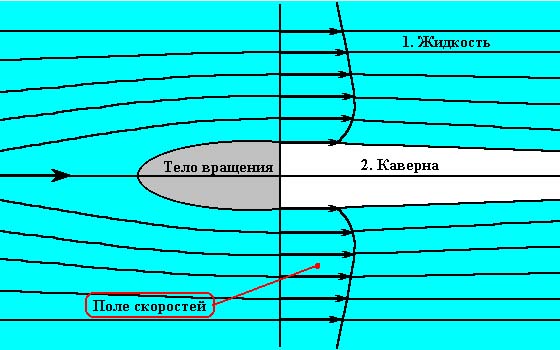
Дальше по мтодике расчёта (лишь для этих малых радиусов) с ростом V увеличивается Hп, α° и соответственно Hв, без изменения Δα° - оптимального угла атаки.
Дальнейшие поправки к углу атаки, это поправки на индуктивную поступь и поправка Прантля-Гольдштейна на телесность каверны не делались, так как профиль выбирался с неизвестными гидродинамическими характеристиками. Угол атаки выбирался сразу Δα° = 7° - 8°, описанный в литературе как оптимальный, по результатам испытаний систематических серий суперкавитирующих винтов.
В вверх.
9. Примеры некоторых винтов, изготовленных по такому методу расчёта, и скоростные результаты.
По приведённой выше методике расчётов изготавливались винты методом литья по выплавляемым моделям с последующей обработкой и доводкой лопастей на прилегание к шаговой горке.
Пример 1.
Класс SAN-250, пластиковая мотолодка класса SJ. Максимальная скорость достигнутая с мотором "Ветерок-12" P=1,6[кг/см**2], то есть V=63,5 км/час.
Параметры винта:
D = 216 - 214мм; dст = 60мм; z = 3; Θ = 0,4; распределение хорды лопасти по радиусу по таблице (5.1); Hп = 255мм; Δα° = 7°; распределение толщины лопасти по радиусу линейное (максимальная толщина 4,5мм, минимальная толщина 0,5мм); радиус входящей кромки 0,25мм. Максимум толщины профиля приходится на выходящую кромку. Ось выходящей кромки перпендикулярна оси винта.
Гондола редуктора полностью вынута из воды, вал расположен горизонтально днищу.
Пример 2.
Класс SAN-250, пластиковая мотолодка класса SJ. Максимальная скорость достигнутая с мотором "Ветерок-12" P=1,6[кг/см**2], то есть V=63,5 км/час.
Параметры винта:
D = 216 - 214мм; dст = 60мм; z = 3; Θ = 0,45; распределение хорды лопасти по радиусу по таблице (5.1); Hп = 260мм; Δα° = 7°; распределение толщины лопасти по радиусу линейное (максимальная толщина 4,5мм, минимальная толщина 0,5мм); радиус входящей кромки 0,25мм. Максимум толщины профиля приходится на выходящую кромку. Ось выходящей кромки перпендикулярна оси винта.
Гондола редуктора полностью вынута из воды, вал расположен горизонтально днищу.
В процессе доводки на винт наколачивался интерцептор. Скорость без интерцептора составила P=1,5[кг/см**2], с интерцептором скорость составила P=1,6[кг/см**2], но при этом мотор пришлось поднять вверх на 5мм.
Пример 3.
Класс SBN-350, пластиковая мотолодка класса SB ("Эпсилон"). Максимальная скорость с мотором "Привет-22" составила P=2,2[кг/см**2], или V=74,5 км/час.
Параметры винта:
D = 240 - 235мм; dст = 60мм; z = 3; Θ = 0,4; Hп = 267мм; Δα° = 7°; распределение хорды лопасти по радиусу в таблице(9.1).
| ____r___ | 35 | 45 | 55 | 65 | 75 | 85 | 95 | 105 | 115 |
|---|---|---|---|---|---|---|---|---|---|
| ___br___ | __58__ | __63__ | __64__ | _63,5_ | __60__ | __54__ | __46__ | __35__ | __19__ |
Распределение толщины лопасти по радиусу линейное (максимальная толщина 4,5мм, минимальная толщина 0,5мм); радиус входящей кромки 0,25мм. Максимум толщины профиля приходится на выходящую кромку. Ось выходящей кромки перпендикулярна оси винта.
В вверх.
10. Литература:
-
1. Хейфец Л.Л.
X35 Гребные винты для катеров - 2-е издание, переработанное и дополненное- Л.: Судостроение, 1980-200с.
2. С-74 Справочник по теории корабля в трёх томах. Том 3. Управляемость водоизмещающих судов. Лидродинамика судов с гидродинамическими принципами поддержания/Под ред. Я.И.Войкутовского. - Л.: Судостроение, 1985 - 544с, ил
3. Д23 Движители быстроходных судов/М.А.Мавлюдов, А.АюРусецкий, Ю.М.Садовников, Э.А.Фишер. - 2-е изд., перераб и доп - Судостроение, 1982-280с ИСБН
4. Т45 Титов И.А., Егоров И.Т., Дробленков В.Ф. Ходкость быстроходных судов. - Л.: Судостроение, 1979, 256с., ил.
5. Сборник "Катера и яхты".
6. УДК 629.12.075(075.8)
Ходкость и управляемость судов. Басин А.М. Учебное пособие для вузов водн. трансп. М.,"Транспорт", 1977.456с.
В вверх.